JPEG算法解密（二）

thejinchao

步骤三：离散余弦变换

---

        这次我们来介绍JPEG算法中的核心内容，离散余弦变换（Discrete cosine transform），简称DCT。
        离散余弦变换属于傅里叶变换的另外一种形式，没错，就是大名鼎鼎的傅里叶变换。傅里叶是法国著名的数学家和物理学家，1807年，39岁的傅里叶在他的一篇论文里提出了一个想法，他认为任何周期性的函数，都可以分解为为一系列的三角函数的组合，这个想法一开始并没有得到当时科学界的承认，比如当时著名的数学家拉格朗日提出质疑，三角函数无论如何组合，都无法表达带有“尖角”的函数，一直到1822年拉格朗日死后，傅里叶的想法才正式在他的著作《热的解析理论》一书中正式发表。
        金子总会闪光，傅里叶变换如今广泛应用于数学、物理、信号处理等等领域，变换除了它在数学上的意义外，还有其哲学上的伟大意义，那就是，世上任何复杂的事物，都可以分解为简单的事物的组合，而这个过程只需要借助数学工具就可以了。但是当年拉格朗日的质疑是正确的，三角函数的确无法表达出尖角形状的函数，不过只要三角函数足够多，可以无限逼近最终结果。比如下面这张动图，就动态描述了一个矩形方波，是如何做傅里叶分析的。

        当我们要处理的不再是函数，而是一堆离散的数据时，并且这些数据是对称的话，那么傅里叶变化出来的函数只含有余弦项，这种变换称为离散余弦变换。举个例子，有一组一维数据[x0,x1,x2,...,xn-1],那么可以通过DCT变换得到n个变换级数Fi

(2.1)

        此时原始数据Xi可以通过离散余弦变换变化的逆变换（IDCT)表达出来

(2.2)

        也就是说，经过DCT变换，可以把一个数组分解成数个数组的和，如果我们数组视为一个一维矩阵，那么可以把结果看做是一系列矩阵的和

(2.3)

        举个例子，我们有一个长度为8的数字，内容为50,55,67,80,-10,-5,20,30，经过DCT转换，得到8个级数为287.0,106.3,14.2,-110.8,9.2,65.7,-8.2,-43.9，根据公式2.3把这个数组转换为8个新的数组的和，如果我们使用图像来表达的话，就可以发现DCT转换的有趣之处了

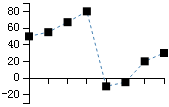
[50,55,67,80,-10,-5,20,30]
		数组0
			[35.9,35.9,35.9,35.9,35.9,35.9,35.9,35.9]
		数组1
			[26.0,22.1,14.8,5.2,-5.2,-14.8,-22.1,-26.1]
		数组2
			[3.3,1.4,-1.4,-3.3,-3.3,-1.4,1.4,3.3]
		数组3
			[-23.0,5.4,27.2,15.4,-15.4,-27.2,-5.4,23.0]
		数组4
			[1.6,-1.6,-1.6,1.6,1.6,-1.6,-1.6,1.6]
		数组5
			[9.1,-16.1,3.2,13.6,-13.6,-3.2,16.1,-9.1]
		数组6
			[-0.8,1.9,-1.9,0.8,0.8,-1.9,1.9,-0.8]
		数组7
			[-2.1,6.1,-9.1,10.8,-10.8,9.1,-6.1,2.1]

        奥妙之处在于，经过DCT，数据中隐藏的规律被发掘了出来,杂乱的数据被转换成几个工整变化的数据。DCT转换后的数组中第一个是一个直线数据，因此又被称为“直流数据”，简称DC，后面的数据被称为“交流数据”，简称AC，这个称呼起源于信号分析中的术语。

        在JPEG压缩过程中，经过颜色空间的转换，每一个8X8的图像块，在数据上表现为3个8X8的矩阵，紧接着我们对这三个矩阵做一个二维的DCT转换，二维的DCT转换公式为

(2.1)

        DCT的威力究竟有多大，我们可以做一个实际的测试，比如一个所有数值都一样的矩阵，经过DCT转换后，将所有级数组合成一个新的矩阵

        可以看到，经过DCT转换，矩阵的“能量”被全部集中在左上角上的直流分量F(0,0）上，其他位置都变成了0。
        在实际的JPEG压缩过程中，由于图像本身的连贯性，一个8X8的图像中的数值一般不会出现大的跳跃，经过DCT转换会有类似的效果，左上角的直流分量保存了一个大的数值，其他分量都接近于0，我们以Lenna左上角第一块图像的Y分量为例，经过变换的矩阵为

        可以看到，数据经过DCT变化后，被明显分成了直流分量和交流分量两部分，为后面的进一步压缩起到了充分的铺垫作用，可以说是整个JPEG中最重要的一步。

有些地方格式乱掉了，原文发表于我的博客

oathupdate

看晕了 数学渣路过