在渲染中制造真实的水面波动效果：波动方程

小篱

文/寂灭万乘

很多游戏描述的世界都会含有流体表面，他们可能是个水池，可能是桶强酸，或者一个熔岩坑。为使这些对象的表面如同物理世界一样，需要模拟波在液体表面的扰动传播方式。

水池

波动方程

波动方程是一个偏微分方程，表示为在恒定张力下的一维线或二维面上每一个点的运动方式

一维线波动方程为：

c为波速，x,y是二维笛卡尔坐标系的2个维

二维面波动方程为

z为x,y轴构成平面的第三维

由于波速会因为粘性阻尼力衰减，所以水面的波动方程如下

u为液体粘稠度，用以控制波在液体表面的存在时间

近似导数

实时仿真波动方程需要大量的计算，所以使用近似导数简化方程

近似导数如下

所以可得

同理

计算液体表面平移

由之前的近似表达式易得

使dx=dy=d易得最终方程如下

稳定条件

如果波速c太快，或者dt时间段太长，使位移发散为无穷大，需要约束c或t，约束如下

（ ）

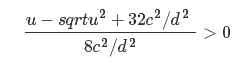
或

（ ）

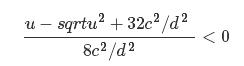
参考资源

Mathematics for 3D Game Programming and Computer Graphics,Third Edition

博客地址：https://www.cnblogs.com/millionsmultiplication/p/9895079.html