本帖最后由 smallcorpse 于 2013-10-27 16:57 编辑
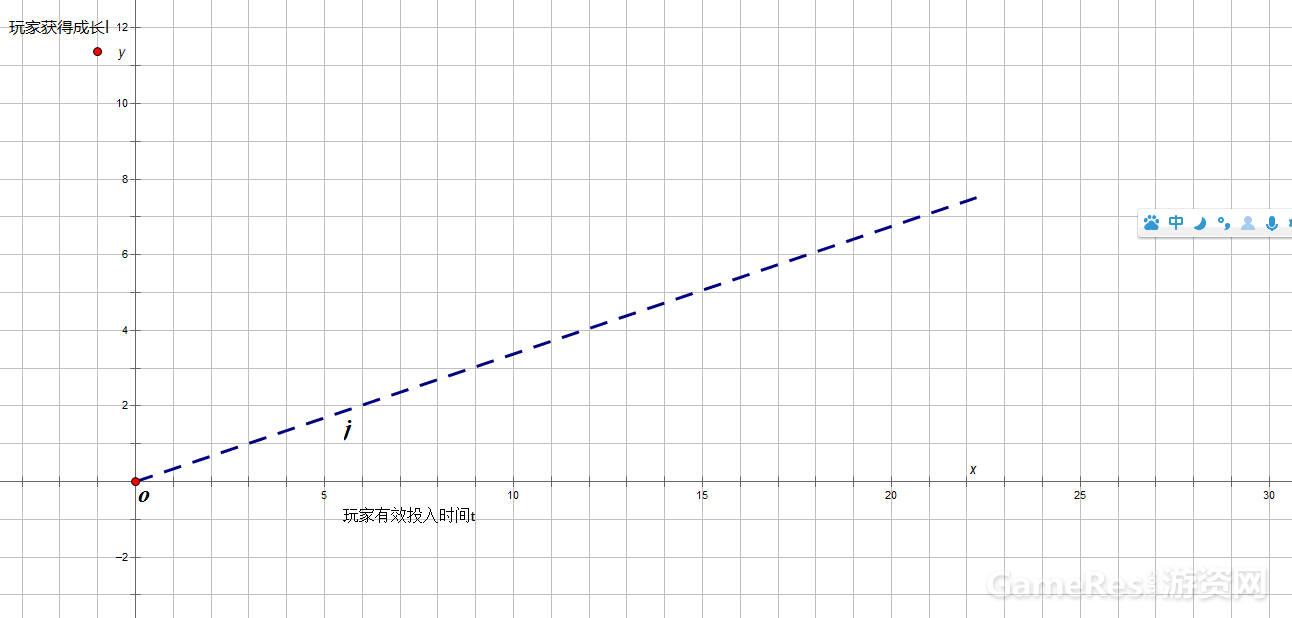
上图是一个MMORPG中一个玩家的成长模型,当然这个模型不是通用的,有些游戏使用的是倒数曲线,有的是双曲线,各有利弊,我这个主要是因为画起来方便(笑)。
玩家有效投入时间,指的是玩家在游戏进行过程中完成设计者设定的关卡所投入的时间。
玩家获得成长,指的是玩家在游戏进行过程中完成设计者设定的关卡后所获得的成长,包括但不限于等级经验的提示、属性的增强。
其中,设计者设定的关卡包括但不限于任务、副本、竞技场。具体释义请参照百度百科“关卡”词条中游戏关卡的释义。
倒数曲线的成长指的是随着玩家有效投入时间t的增加,在单位时间内玩家获得的成长l逐步减少,利在成长上限可控,弊在游戏后期老板说要加点明显的成长,比如加点资料片啥的你就得打补丁了。
双曲线的成长指的是随着玩家有效投入时间t的增加,在单位时间内玩家获得的成长l逐步增加,利在快感丛生,数字越来越大,而且不怕老板说要加成长,弊在后期数字真的太大了,有种控制不住的感觉。
直线的成长最简单,随着玩家有效有效投入时间t的增加,在单位时间内玩家获得的成长l不变,利在画起来简单,而且用起来也简单,弊在成长上限不可控,对玩家来说也没有大数字快感的刺激(集以上两个曲线的缺点大成)。
选择好了成长模型,还没完,到了引入关卡难度概念了,没有关卡难度,数字再大也体现不出成长。
关卡的难度,理论上来说是要略比玩家获得的成长大一点点的。
为什么呢,因为玩家除了系统里获得的数值上的成长,还有一个成长是在游戏中体现不出来了:对游戏的熟悉度。也就是说成长曲线l(t)只描述了玩家获得的数值上的成长,实际上玩家获得的成长包括游戏熟悉度,如果转化为游戏中等效的数值,是大于l(t)的。这也解释了为什么游戏设计者按照系统内玩家成长相应设计关卡难度时,越到游戏后期会让玩家觉得越简单的原因。
根据以上缘由,关卡设计难度与玩家成长曲线的差值r(t)-l(t)需要与t相关,不能是一个常数。
那我就再加一条斜率大点的直线(笑),另外两个曲线也可以同理加一条,在此就不赘述了。
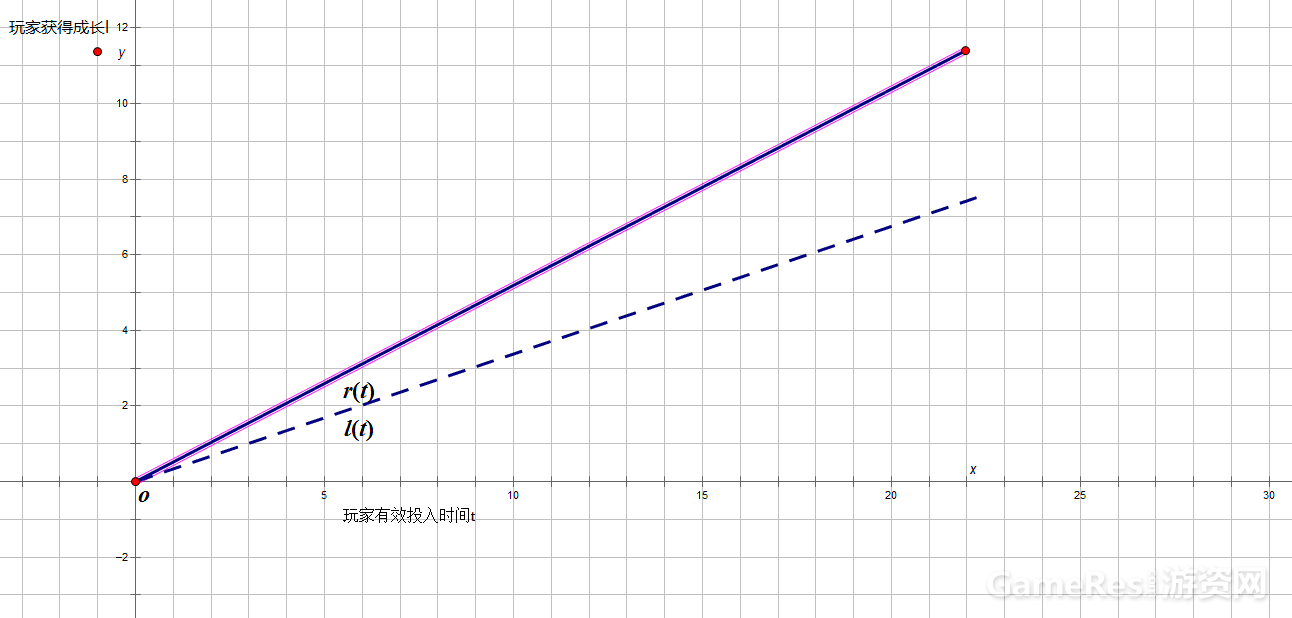
写到这,这个模型就算完事儿了么,这个只能算是战略上的模型,我们还得细化一下战术层面上的模型。
现在开始引入策略的概念,也就是博弈中的策略概念,大家放心,不会涉及到什么纳什平衡、帕累托最优这种让人毁三观的理论,仅仅把策略的定义引用进来。
策略(strategies):一局博弈中,每个局中人都有选择实际可行的完整的行动方案,即方案不是某阶段的行动方案,而是指导整个行动的一个方案,一个局中人的一个可行的自始至终全局筹划的一个行动方案,称为这个局中人的一个策略。如果在一个博弈中局中人都总共有有限个策略,则称为“有限博弈”,否则称为“无限博弈”。(摘自维基百科“博弈论”词条)
运用到游戏中,我们定义玩家在面临一次选择时,叫做一局博弈,也就是说,技能1,技能2,技能3,我选哪一个去糊对面boss的脸,这就叫一局博弈(好像有点分太细了,不要紧,就这么着)。 假设玩家在进行一次关卡流程时需要面临n次选择,举例来说就是打个boss要释放n个技能,也就是说进行n局博弈。 在此又引入零和博弈的概念。
零和博弈(英语:Zero-Sum Game),又称零和游戏或零和赛局,与非零和博弈相对,是博弈论的一个概念,属非合作博弈。指参与博弈的各方,在严格竞争下,一方的收益必然意味着另一方的损失,博弈各方的收益和损失相加总和永远为“零”,双方不存在合作的可能。(摘自维基百科“零和博弈”词条)
假设这类博弈是零和博弈(其实不用假设,打个boss还有双赢的可能么),那么在这n局博弈中,玩家有m局胜利了获得了收益。那么我们定义m/n为玩家对游戏的熟悉度a(t)。(acquaince)
玩家的熟悉度被数值化出来后,我们就可以对关卡设计难度与玩家成长曲线的差值r(t)-l(t)进行规范了。
因为玩家对游戏的熟悉度a(t)是一个比率,所以我们定义在n局博弈中平均每次胜利所获得收益为b。(benefit)
那么玩家由于对游戏的熟悉度等效转化为游戏中的成长即为a(t)*b。大家注意,b可能是一个与时间相关的变量,也可能是一个常量,这就靠游戏设计者怎么拍脑袋了。
一般而言,玩家对游戏的熟悉度因人而异,所以在游戏设计者考虑玩家对游戏的熟悉度通常是按档次来的。比如特别不熟悉,有点熟悉,比较精通,精通等 。 好不容易把熟悉度数值化了当然不可能回到老路上去(笑)。我们设定,在一个关卡中,玩家熟悉度达到了A,那么就表明他通过了此关卡,这个A可能是一个与时间相关的变量,也可能是一个常量。看游戏设计者怎么拍脑袋了。
我是这样拍脑袋的。 其中实线线段是表明关卡难度,OA的值表示的是上文所说的A。也就是说,每过一段时间内之后,玩家都需要对游戏熟悉度成长一个定值。
这个模型有个天大的问题,a(t)*b是有上限的,因为a∈[0,1],那么就是说,如果按这个模型来看,一般玩家进行到一定时间段,就无法通过增加游戏熟悉度而通过关卡了。
如果把这个一般玩家变成免费玩家……(偷笑),老板这时候是不是该给我加工资了。
其实,游戏关卡难度和玩家有效投入时间并不是处以同一个时间轴上的。也就是说游戏关卡难度不会随着玩家投入时间的增长而增长,他们是不相干的,我只是画着方便而已,各位看官就不要扇我脸了。
其实一般玩家进行到一定时间段如果被游戏关卡难度所卡住的话,也可以将整个坐标轴平移,也就是通过投入更多的有效时间获得更多成长后通过关卡。
结语:有人会说以上这个东西大家都懂,你这写的毫无意义,对此我不置可否。撰写本文的目的只是为了剖析实际真谛,虽然说可能目的并没有达到。但是如果没有人开这个头,游戏业永远只会停留于“经验论”,“资历论”上。我的目的是希望更多的游戏从业者站出来以学者的角度剖析事件寻求真理。
《如何让一个游戏程序变成一个游戏产品,论用户体验》这个帖子比另外写的两个骂战贴个人感觉有用多了,希望多关注交流一下。
谢谢收看,我们再见。 | 