文/腾讯互娱工程师-王杰
一、服务器CPU性能优化
1.1寻路算法JPS优化
MMORPG游戏中服务器中需要对NPC寻路,然而A*算法及其各种优化并不让人满意,因此寻路算法也成为瓶颈之一。
因此,本文介绍JPS的效率、多线程、内存、路径优化算法。为了测试搜索算法的优化性能,实验中设置游戏场景使得起点和终点差距200个格子,需要寻路104次。结果发现,A*寻路总时间约2.6074x1011纳秒(一秒为109纳秒);基础版JPS寻路总时间1.7037x1010纳秒;利用位运算优化的JPS(下文称JPS-Bit)寻路总时间3.2364x109纳秒;利用位运算和剪枝优化的JPS(下文称JPS-BitPrune)寻路总时间2.3703x109纳秒;利用位运算和预处理的JPS(下文称JPS-BitPre)寻路总时间2.0043x109纳秒;利用位运算、剪枝和预处理三个优化的JPS(下文称JPS-BitPrunePre)寻路总时间9.5434x108纳秒。
上述结果表明,寻路200个格子的路径,JPS的五个版本,平均消耗时间分别为1.7毫秒、0.32毫秒、0.23毫秒、0.02毫秒、0.095毫秒,寻路速度分别为A*算法的15倍、81倍、110倍、130倍、273倍,大幅度超越A*算法,标志着寻路已经不会成为性能的瓶颈。
事实上,在2012到2014年举办的三届(目前为止只有三届)基于Grid网格寻路的比赛GPPC(The Grid-Based Path Planning Competition)中,JPS已经被证明是基于无权重格子,在没有预处理的情况下寻路最快的算法。
1.1.1 JPS算法介绍
JPS又名跳点搜索算法(Jump Point Search),是由澳大利亚两位教授于2011年提出的基于Grid格子的寻路算法。A*算法整体流程如表1.1.1.1.1所示,JPS算法在保留A*算法的框架的同时,进一步优化了A*算法寻找后继节点的操作。为了说明JPS在A*基础上的具体优化策略,我们在图1.1.1.1.1中给出A*和JPS的算法流程图对比。由图1.1.1.1.1看出,JPS与A*算法主要区别在后继节点拓展策略上,不同于A*算法中直接获取当前节点所有非关闭的可达邻居节点来进行拓展的策略,JPS根据当前结点current的方向、并基于跳点的策略来扩展后继节点,遵循“两个定义、三个规则”(见表1.1.1.1.2,两个定义确定强迫邻居、跳点,三个规则确定节点的拓展原则),具体流程如下:
一,若current当前方向是直线方向:
(1)如果current左后方不可走且左方可走(即左方是强迫邻居),则沿current左前方和左方寻找不在closedset的跳点;
(2)如果current当前方向可走,则沿current当前方向寻找不在closed集合的跳点;
(3)如果current右后方不可走且右方可走(右方是强迫邻居),则沿current右前方和右方寻找不在closedset的跳点;
二,若current当前方向为对角线方向:
(1)如果current当前方向的水平分量可走(例如current当前为东北方向,则水平分量为东),则沿current当前方向的水平分量寻找不在closedset的跳点;
(2)如果current当前方向可走,则沿current当前方向寻找不在closedset的跳点;
(3)如果current当前方向的垂直分量可走(例如current当前为东北方向,则垂直分量为北),则沿current当前方向的垂直分量寻找不在closedset的跳点。
JPS寻找跳点的过程有三种优化:一,位运算;二;预处理;三;剪枝中间跳点。
图1.1.1.1.1A*和JPS的算法流程图对比
表1.1.1.1.1 A*算法流程:
Step 1. 将起始点start加入开启集合openset
Step 2. 重复以下工作:
当openset为空,则结束程序,此时没有路径。
寻找openset中F值最小的节点,设为当前点current
从openset中移出当前点current
关闭集合closedset中加入当前点current
若current为目标点goal,则结束程序,此时有路径生成,此时由goal节点开始逐级追溯路径上每一个节点x的上一级父节点parent(x),直至回溯到开始节点start,此时回溯的各节点即为路径。
对current的八个方向的每一个相邻点neighbor
如果neighbor不可通过或者已经在closedset中,略过。
如果neighbor不在openset中,加入openset中
如果neighbor在openset中,G值判定,若此路径G值比之前路径小,则neighbor的父节点为current,同时更新G与F值。反之,则保持原来的节点关系与G、F值。G值表示从起点到当前点路径耗费;H值表示不考虑不可通过区域,当前点到终点的理论路径耗费;F=G+H。
| 术语参考:
| current
| 当前节点
| openset
| 开启节点集合,集合内节点有待进一步探索拓展
| closedset
| 关闭节点结合,集合内节点后续不再进行拓展
| neighbor
| 邻居,与当前节点相邻的节点
| parent(x)
| 节点x的父节点,即算法寻得的路径中节点parent(x)的下一节点为x
|
表1.1.1.1.2 JPS算法的“两个定义、三个规则”:
定义一,强迫邻居(forced neighbour):如果点n是x的邻居,并且点n的邻居有阻挡(不可行走的格子),并且从parent(x)、x、n的路径长度比其他任何从parent(x)到n且不经过x的路径短,其中parent(x)为路径中x的前一个点,则n为x的强迫邻居,x为n的跳点),例如图2中,寻找从S到E的路径时,K为I的强迫邻居(I为K的跳点)。这里不认为从H到K能走,因为对角线有阻挡(这点和论文不一致,但和代码一致,因为如果H到K能直接到达,会走进H右边的阻挡区,大部分的JPS开源代码根据论文都认为H到K能走,所以存在穿越阻挡的情况),如果需要H到K可走,则K为H的强迫邻居(H为K的跳点)。
定义二,跳点(jump point):(1)如果点y是起点或目标点,则y是跳点,例如图2中,S是起点也是跳点,E是目标点也是跳点;(2)如果y有邻居且是强迫邻居则y是跳点, 例如I是跳点,请注意此类跳点和强迫邻居是伴生关系,从上文强迫邻居的定义来看n是强迫邻居,x是跳点,二者的关系是伴生的,例如图2中K的邻居只有I是跳点,M虽然也是K的邻居,但M不是跳点,因为K不是M的强迫邻居;(3)如果parent(y)到y是对角线移动,并且y经过水平或垂直方向移动可以到达跳点,则y是跳点,例如图2中G是跳点,因为parent(G)为S,S到G为对角线移动,从G到跳点I为垂直方向移动,I是跳点,所以G也是跳点。
规则一,JPS搜索跳点的过程中,如果直线方向(为了和对角线区分,直线方向代表水平方向、垂直方向,下文所说的直线均为水平方向和垂直方向)、对角线方向都可以移动,则首先在直线方向搜索跳点,再在对角线方向搜索跳点。
规则二,(1)如果从parent(x)到x是直线移动,n是x的邻居,若有从parent(x)到n的路径不经过x且路径长度小于或等于从parent(x)经过x到n的路径,则走到x后下一个点不会走到n;(2)如果从parent(x)到x是对角线移动,n是x的邻居,若有从parent(x)到n的路径不经过x且路径长度小于从parent(x)经过x到n的路径,则走到x后下一个点不会走到n(相关证明见论文)。
规则三,只有跳点才会加入openset,因为跳点会改变行走方向,而非跳点不会改变行走方向,最后寻找出来的路径点也只会是跳点集合的子集。
|
1.1.1.2 JPS算法举例
S
| F
|
|
| E
| A
| G
|
|
| O
| B
| H
|
|
| P
| C
| I
| K
| M
| Q
| D
| J
| L
| N
| R
|
图1.1.1.2.1寻路问题示例场景(5*5的网格)
下面举例说明JPS具体的寻路流程。问题示例如图1.1.1.2.1所示,5*5的网格,黑色代表阻挡区,S为起点,E为终点。JPS要寻找从S到E的最短路径,首先初始化将S加入openset。从openset取出F值最小的点S,并从openset删除,加入closedset,S的当前方向为空,则沿八个方向寻找跳点,在该图中只有下、右、右下三个方向可走,但向下遇到边界,向右遇到阻挡,因此都没有找到跳点,然后沿右下方向寻找跳点,在G点,根据上文定义二的第(3)条,parent(G)为S,praent(G)到S为对角线移动,并且G经过垂直方向移动(向下移动)可以到达跳点I,因此G为跳点,将G加入openset。从openset取出F值最小的点G,并从openset删除,加入closedset,因为G当前方向为对角线方向(从S到G的方向),因此在右、下、右下三个方向寻找跳点,在该图中只有向下可走,因此向下寻找跳点,根据上文定义二的第(2)条找到跳点I,将I加入openset。从openset取出F值最小的点I,并从openset删除,加入closedset,因为I的当前方向为直线方向(从G到I的方向),在I点时I的左后方不可走且左方可走,因此沿下、左、左下寻找跳点,但向下、左下都遇到边界,只有向左寻找到跳点Q(根据上文定义二的第(2)条)),因此将Q加入openset。从openset取出F值最小的点Q,并从openset删除,加入closedset,因为Q的当前方向为直线方向,Q的左后方不可走且左方可走,因此沿右、左、左上寻找跳点,但向右、左上都遇到边界,只有向左寻找到跳点E(根据上文定义二的第(1)条)),因此将E加入openset。从openset取出F值最小的点E,因为E是目标点,因此寻路结束,路径是S、G、I、Q、E。
注意,本文不考虑从H能走到K的情况,因为对角线有阻挡(这点和论文不一致,但和代码一致,因为如果H到K能直接到达,会走进H右边的阻挡区,大部分的JPS开源代码根据论文都认为H到K能直接到达,所以存在穿越阻挡的情况),如果需要H到K能走,则路径是S、G、H、K、M、P、E,修改跳点的计算方法即可。
上述的JPS寻路效率是明显快于A*的,原因在于:在从S到A沿垂直方向寻路时,在A点,如果是A*算法,会将F、G、B、H都加入openset,但是在JPS中这四个点都不会加入openset。对F、G、H三点而言,因为从S、A、F的路径长度比S、F长,所以从S到F的最短路径不是S、A、F路径,同理S、A、G也不是最短路径,根据上文规则二的第(1)条,走到A后不会走到F、G,所以F、G不会加入openset,虽然S、A、H是S到H的最短路径,但因为存在S、G、H的最短路径且不经过A,据上文规则二的第(1)条,从S走到A后,下一个走的点不会是H,因此H也不会加入openset;对B点而言,根据上文规则三,B不是跳点,也不会加入openset,直接走到C即可。
表1.1.1.2.1所示为A*和JPS在寻路消耗中的对比,D.Age:Origins、D.Age 2、StarCraft为三个游戏龙腾世纪:起源、、龙腾世纪2、星际争霸的场景图集合,M.Time表示操作openset和closedset的时间,G.Time表示搜索后继节点的时间。可见A*大约有58%的时间在操作openset和closedset,42%时间在搜索后继节点;而JPS大约14%时间在操作openset和closedset,86%时间在搜索后继节点。避免在openset中加入太多点,从而避免过多的维护最小堆是JPS比A*快的原因((最小堆插入新元素时间复杂度log(n),删除最小元素后调整堆,时间复杂度也为log(n))),实际上在从S到E的寻路过程中,进入openset的只有S、G、I、Q、E
表1.1.1.2.1 A*和JPS的寻路消耗对比
1.1.2 JPS五个优化算法
1.1.2.1 JPS优化之一JPS-Bit:位运算优化
利用位运算优化的JPS-Bit的关键优化思路在于利用位运算来优化JPS中节点拓展的效率。下面以图1.1.2.1.1中的场景示例说明如何将位运算融合于JPS算法中,其中黑色部分为阻挡,假设当前位置为I(标蓝位置),当前方向为右,位运算中使用1代表不可走,0代表可走,则I当前行B的八位可以用八个bit:00000100表示,I上一行B-的八位可以用八个bit:00000000表示,I的下一行B+的八位可以用八个bit:00110000表示。在当前行寻找阻挡的位置可以用CPU的指令__builtin_clz(B)(返回前导0的个数),即当前阻挡在第5个位置(从0开始)。寻找当前行的跳点可以用__builtin_clz(((B->>1)&&!B-)||((B+>>1)&&!B+))寻找,例如本例中(B+>>1)&&!B+为:(00110000>>1)&&11001111,即00001000,而(B->>1)&&!B为00000000,所以__builtin_clz(((B->>1)&&!B-)||((B+>>1)&&!B+))为__builtin_clz(00001000)为4,所以跳点为第4个位置M(从0开始)。注意论文中使用_builtin_ffs(((B-<<1)&&!B-)||((B+<<1)&&!B+)),__builtin_ffs(x)返回x的最后一位1是从后向前第几位,比如7368(1110011001000)返回4,因为论文对格子的bit编码采用小端模式,而这里对格子的bit编码采用大端模式。
由于JPS-Bit使用运算效率更高的位运算和CPU指令运算来优化原始JPS节点扩展过程中的遍历操作,JPS-Bit的算法效率高于原始的JPS,实测中JPS-Bit的寻路时间比JPS缩短5倍左右。
A
| B
| C
| D
| E
| F
| G
| H
| I
| J
| K
| L
| M
|
| N
| O
| P
| Q
|
|
| R
| S
| T
| U
|
图1.1.2.1.1寻路问题示例场景(3*8的网格)
1.1.2.2 JPS优化之二JPS-BitPrune:位运算与剪枝优化
利用位运算和剪枝优化的JPS-BitPrune在JPS-Bit的基础上进一步进行剪枝优化,剪掉不必要的中间跳点(见表1.1.1.1.2,定义二第(3)条定义),根据定义二,中间跳点在节点拓展过程中只具有简单的“承接”作用,不具备拓展价值,将中间跳点放入openset会增大扩展的次数,因此JPS-BitPrune将中间跳点全部删除,将中间跳点后继跳点中的非中间跳点的父跳点改为中间跳点的父跳点,可以有效避免冗余的节点拓展运算。
拐点获取:值得一提的是,JPS-BitPrune由于删除了中间跳点,因此JPS-BitPrune需要在搜索到完整的路径之后以一定的策略在最后寻得的路径中加入中间拐点,使得每两个相邻的路径节点之间都是垂直、水平、对角线方向可达的。对此,JPS-BitPrune采用的具体方法如下:
假设目前搜索到的路径为start(jp1)、jp2、jp3...jpk..end(jpn),对每两个相邻的跳点jpi、jpi+1,一,如果jpi、jpi+1的x坐标或者y坐标相等,说明这两个跳点在同一个水平方向或垂直方向,可以直线到达,无需在这两个跳点之间加入拐点;二,如果jpi、jpi+1的x坐标和y坐标都不相等,(1)如果x坐标的差dx(即jpi的x坐标减去jpi+1的x坐标)和y坐标的差dy的绝对值相等,说明这两个跳点在对角线方向,也可以直线到达,无需在这两个跳点之间加入拐点;(2)如果x坐标的差dx和y坐标的差dy的绝对值不相等,说明这两个跳点不在对角线方向,并且有可能不能直线到达(因为跳点附近有阻挡),此时jpi、jpi+1之间只需要加入一个从jpi出发离jpi+1最近的对角线上的点即可(jpi、jpi+1不能水平、垂直、对角线到达,说明jpi、jpi+1之间一定存在被剪枝的中间跳点,只需要补上离jpi+1最近的一个中间跳点充当拐点即可,该拐点即为jpi沿对角线方向走min(dx,dy)步到达的点)。
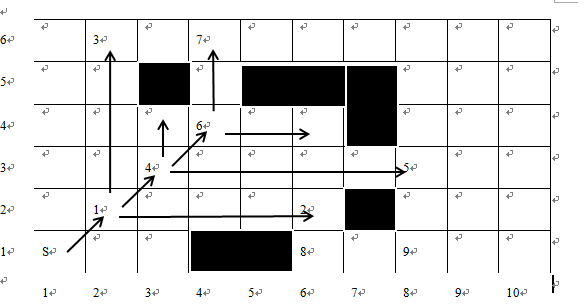
图1.1.2.2.1 JPS-BitPrune的剪枝优化示例
下面以图1.1.2.2.1的问题场景示例JPS-BitPrune如何在剪枝的同时进行寻路。起点为S(坐标为(1,1),即S(1,1)),节点1、4、6均为中间跳点:因为节点2、3是满足定义二第(2)条的跳点,所以节点1是为了到达节点2、3的中间跳点,同理节点4、6也为中间跳点。在剪枝中间跳点之前,要将中间跳点的后继节点的父节点调整为该中间跳点的父节点。例如图1.1.2.2.1中,节点1的后继跳点为节点2、3、4,其中节点4也为中间跳点,删掉中间跳点中的节点1后,节点2、3的父跳点由节点1改为节点S,删除中间跳点中的节点4后,节点4的后继跳点5的父跳点由节点4改为节点S(节点4的父跳点为节点1,但节点1已经被删掉,因此回溯到节点S),删除中间跳点中的节点6后,节点6的后继跳点7的父跳点由节点6改为节点S(节点6的父跳点为节点4,但节点4被删,节点4的父跳点节点1也被删,因此回溯到节点S)。
上述过程是简化的逻辑描述,实际运行中的做法是从节点S寻找跳点,首先找到中间跳点节点1,然后在水平方向和垂直方向寻找到跳点节点2、3,将节点2、3的父跳点设为节点S;继续沿对角线方向寻找跳点,走到节点4后,沿水平方向和垂直方向寻找到跳点节点5,将节点5的父跳点设为节点S;继续沿对角线方向寻找跳点,走到节点6后,沿水平方向和垂直方向寻找到跳点7,将跳点7的父跳点设为节点S。因此JPS-BitPrune获得路径S(1,1)、节点7(4,6)。
因为路径中S(1,1)无法垂直、水平、对角线方向走到节点7(4,6),需要加入中间拐点,根据上述的拐点添加策略,有dx为3,dy为5,需要从S沿对角线走3步,即节点6(4,4)可作为中间拐点,因此,在图1.1.2.2.1的示例中,JPS-BitPrune最后构建的完整路径为S(1,1)、节点6(4,4)、节点7(4,6)。
1.1.2.2.1剪枝的优化效率
下面通过对比剪枝前后的JPS节点拓展的情况来说明剪枝操作的优化效率:
场景一(无剪枝)如果不对中间跳点进行剪枝,那么从节点S寻路到节点7将经历如下过程:
从节点S搜索跳点,找到跳点节点1,openset此时只有节点1;
从openset取出F值最小跳点节点1,并搜索节点1的后继跳点,水平方向和垂直方向找到跳点节点2、3,对角线方向找到跳点节点4,此时openset有节点2、3、4;
从openset取出F值最小跳点节点4,并搜索节点4的后继跳点,水平和垂直方向找到跳点节点5,对角线方向找到跳点6,此时openset有节点2、3、5、6;
从openset取出F值最小跳点节点6,垂直方向找到跳点7,此时openset有节点2、3、5、7;
从openset取出F值最小的跳点节点7,为目的点,搜索结束,因此完整路径为节点S(1,1)、节点1(2,2)、节点4(3,3)、节点6(4,4)、节点7(4,6)。JPS在到达目的节点7之前,需要接连拓展中间跳点1,4,6。
场景二(剪枝中间跳点)在剪枝中间跳点之后,从节点S寻路到节点7的流程得到了明显简化:
从节点S寻找跳点,首先找到中间跳点节点1,然后在水平方向和垂直方向寻找到跳点节点2、3,将节点2、3的父跳点设为节点S;继续沿对角线方向寻找跳点,走到节点4后,沿水平方向和垂直方向寻找到跳点节点5,将节点5的父跳点设为节点S;继续沿对角线方向寻找跳点,走到节点6后,沿水平方向和垂直方向寻找到跳点7,将跳点7的父跳点设为节点S;继续沿对角线方向寻找跳点,遇到阻挡,搜索终止,此时openset有节点2、3、5、7;
从openset取出F值最小的跳点节点7,为目的点,搜索结束,此时获得的路径为S(1,1)、节点7(4,6)。不同于无剪枝的JPS需要拓展中间跳点1、4、6,在JPS-BitPrune中,节点1、4、6作为中间跳点均被剪枝,有效避免了冗余的节点拓展,寻路效率得到大大提升。
1.1.2.3 JPS优化之三JPS-BitPre:位运算与预处理
本优化中的预处理在一些文章被称为JPS+。JPS-BitPre和JPS-BitPrunePre都不支持动态阻挡,因为动态阻挡的出现会导致八个方向最多能走的步数发生变化,从而导致预处理的结果不再准确。利用位运算和预处理的JPS-BitPre依旧采用JPS-Bit中的位运算,而其中的预处理则是对每个点存储八个方向最多能走的步数step,这个step值将影响JPS中节点的拓展顺序和拓展“跨度”,加快寻路效率。由于预处理版本的JPS需要存储八个方向最多能走多少步,如果地图大小是N*N,每个方向最多能走的步数用16位数表示,则需要存储空间N*N*8*16bit,如果N为1024,则大概需要存储空间为16M,存储空间占用较大,使用该版本JPS时需要权衡是否以空间换时间,另外预处理的时间对小于1024*1024个格子的图可以在1秒内处理完,但对于2048*2048个格子的图需要一小时左右处理完。
其中,step值由跳点、阻挡、边界等决定,如果遇到跳点,则step为走到跳点的步数;否则step为走到阻挡或边界的步数。
例如对图1.1.2.3.1中的N点,向北最多走到节点8,即2步;
向南最多走到节点4,即4步;
向西最多走到节点6,即3步;
向东最多走到节点2(节点2是满足定义二第(2)条的跳点),即5步;
西北最多走到节点7,即2步;
东北最多走到节点1(节点为1是上文定义二第(3)条定义的跳点),即1步;
西南最多走到节点5,即3步;
东南最多走到节点3(节点3是上文定义二第(3)条定义的跳点),即3步。
7
|
| 7
|
| 8
|
|
|
|
|
| 6
|
|
|
|
| 1
|
|
| 9
|
| 5
| 6
|
|
| N
|
|
|
|
| 2
| 4
|
|
| 11
|
|
|
|
|
|
| 3
|
|
| T
|
|
|
|
|
|
| 2
| 5
|
|
|
|
|
| 3
|
| 10
|
图1.1.2.3.1 JPS-BitPre寻路的场景示例
以图1.1.2.3.1中的场景为例,要寻找从节点N到节点T的路径,JPS-BitPre的寻路流程如下:
从openset取出节点N,从N沿八个方向寻找跳点,根据预处理得到的各方向最远可走的step值,可以快速确定八个方向最远能到达的节点{1,2,3,4,5,6,7,8},如图1.1.2.3.1所示,其中,节点1、2、3均为满足定义二的跳点,直接加入openset,对于节点4、5、6、7、8,首先判断终点T位于以N为中心的南、西南、西、西北、北的哪部分,因为T位于西南方向,只有节点5位于西南方向,因此节点4、6、7、8直接略过,在从N到5的方向上,N可走3步,而N和T的x坐标差绝对值dx为1,y坐标差绝对值dy为2,因此将从节点N到节点5方向上走min(dx,dy)步即节点11,加入openset;
从openset取出F值最小节点11,垂直方向找到跳点T,加入openset;三,从openset取出F值最小节点T,为目的点,搜索结束,此时获得的路径为N(4,5)、节点11(3,4)、节点T(3,3)。
为了说明JPS-BitPre寻路的准确性与高效率,这里给出原始JPS-Bit从N到T的寻路流程作为对比:
从openset取出节点N后,需要沿八个方向寻找跳点,节点1、3、11为上文定义二第(3)条定义的跳点,加入openset,节点2为上文定义二的第(2)条定义的跳点,加入openset;
从openset取出F值最小节点11,垂直方向找到跳点T,加入openset;
从openset取出F值最小跳点T,为目的点,搜索结束,此时获得的路径也为N(4,5)、节点11(3,4)、节点T(3,3)。
对比发现,经过预处理的JPS-BitPre和只使用位运算的JPS-Bit最后寻得的路径是一样的,然而,由于JPS-BitPre无需在每一步节点拓展过程中沿各方向寻找跳点,其可以根据预处理得到的step值快速确定openset的备选节点,从而大大提升寻路效率。
1.1.2.4 JPS优化之四:不可达两点提前判断
如图1.1.2.4.1所示,起点S不可到达终点E,然而寻路算法仍然会花费时间去寻找S、E之间的路径,而且失败情况下寻路花费的时间远大于成功情况下寻路花费的时间,因为失败情况下需要遍历所有的路径,才能确定两点不可达。因此为了避免这种情况,在每次寻路之前,判断起点和终点是否可达:如果起点和终点在同一连通区域,则起点和终点可达,否则不可达。只有起点和终点可达,才需要去寻路。
首先计算Grid网格的连通区域,算法如表1.1.2.4.1所示,算法只能采用宽度优先搜索,深度优先搜索的递归层次太深,会导致栈溢出。按照表1.1.2.4.1的算法,图1.1.2.4.1的点S、1、2的连通区域编号均为1,点3、4、E的连通区域编号均为2,S、E连通区域编号不同,因此S、E不在同一连通区域,不需要寻找路径。表1.1.2.4.1的算法在程序启动时计算一次即可,算法复杂度为O(N),N为Grid网格数目,运行时只需要查询两点是否在同一连通区域,算法复杂度为O(1)。
图1.1.2.4.1不可达的两点S、E
表1.1.2.4.1计算连通区域
Step1. 当前连通区域编号num初始化为0
Step2. 对Grid网格每个点current重复以下工作:
一、 num++。
二、 如果current是阻挡点,跳过。
三、 如果current被访问过,跳过。
四、 current的连通区域编号记为num,标记已访问过。
五、 宽度优先搜索和current四连通的所有Grid网格点,连通区域编号均记为num,
并标记已访问过。
|
1.1.2.5 JPS优化之五:空间换时间
openset采用最小堆实现,最小堆的底层数据结构是一个数组,从最小堆中插入、删除时间复杂度为O(logn)。除了删除还需要查找操作,每次找到一个跳点,都需要判断在最小堆中是否有,如果有,则判断是否更新G值、F值、父跳点等,如果没有,则加入openset。在最小堆的中查找操作时间复杂度O(n),因此需要优化。closedset存的是已经从openset中弹出的跳点,实际只需要对每个跳点加个标记即可,如果跳点打上标记,则表示是closedset中跳点,否则不是。
综合上述需求,针对1km*1km的地图,构建2k*2k的二维数组matrix,数组每个元素pnode均为一个指针,指针的对象类型包括节点id、是否扩展过expanded(即是否在closedset中)、G值、F值、父跳点指针parent、在最小堆中的索引index等12个byte。如果地图(x,y)处是搜索到的跳点,首先检查在二维数组matrix对应的(x,y)处指针pnode是否为空,如果为空,表示该跳点之前未搜索过,从内存池new出一个跳点,将指针加到最小堆openset中,并在执行shift up、shift down操作之后,记录在最小堆中的索引index;如果不为空,则表示该跳点之前搜索过,首先检查expand标记,如果为真,则表示在closedset中,直接跳过该跳点;否则表示在openset中,通过matrix(x,y)记录的在openset中的索引index找到对应的指针,检查matrix(x,y)和openset(index)的指针是否相等进行二次确认,然后检查判断是否需要更新G值、F值、父跳点等,采用空间换时间的方法可以将openset和closedset中查找操作降为O(1)。游戏中有很多场景,无需为每个场景构建一个matrix,以最大的场景的大小构建一个matrix即可。
1.1.3多线程支持
游戏服务器普遍采用单进程多线程架构,多线程下,不能对JPS寻路加锁,否则寻路串行化,失去了多线程的优势,为了支持多线程JPS寻路,需要将一些变量声明为线程独有thread_local,例如上文提到的为了优化openset和closedset的查找速度,构建的二维跳点指针数组matrix。该数组必须为线程独有,否则,不同线程在寻路时,都修改matrix元素指向的跳点数据,例如A线程在扩展完跳点后,将expanded标记为真,B线程再试图扩展该跳点时,发现已经扩展过,就直接跳过,导致寻路错误。
1.1.4 JPS内存优化算法
1.1.4.1分层
JPS的地图格子粒度如果采用0.5m*0.5m,每个格子占1bit,则1km*1km的地图占用内存2k*2k/8个byte,即0.5M;为了向上、向下也能通过取32位数获得向上、向下的32个格子阻挡信息,需要存将地图旋转90度后的阻挡信息;
上文JPS优化之四:不可达两点提前判断,需要存连通信息,假设连通区数目最多15个,则需内存2k*2k/2个byte,即2m,则内存为:原地图阻挡信息0.5m、旋转地图阻挡信息0.5m、连通区信息2m,即3m。另外,上文提到用空间换时间的方法,为了优化openset和closedset的查找速度,构建二维跳点指针数组matrix。1km*1km的地图,格子粒度为0.5m*0.5m,构建出的matrix指针数组大小为2k*2k*4byte即为8m,为了支持多线程,该matrix数组必须为thread_local,即线程独有,16个线程共需内存16*8m即为128m,内存空间太大,因此需要优化这部分内存。
首先将2k*2k分成100*100的块,即20*20个块,20*20个块为第一层数组firLayerMatrix,100*100为第二层数组secLayerMatrix,firLayerMatrix的400个元素为400个指针,每个指针初始化为空,当遍历到的跳点属于firLayerMatrix中(x,y)的块时,则从内存池new出100*100*4byte的secLayerMatrix,secLayerMatrix每个元素也是一个指针,指向一个从内存池new出来的跳点。
例如,搜索2k*2k的地图时,在(231,671)位置找到一个跳点,首先检查firLayerMatrix的(2,6)位置指针是否为空,如果为空,则new出100*100*4byte的secLayerMatrix,继续在secLayerMatrix查找(31,71)位置检查跳点的指针是否为空,如果为空,则从内存池new出来跳点,加入openset,否则检查跳点的expanded标记,如果标记为真,表示在closedset中,直接跳过该点,否则表示在openset中,判断是否更新G值、F值、父节点等。因为游戏中NPC寻路均为短距离寻路,JPS寻路区域最大为80*80,一个secLayerMatrix是100*100,因此只需要一个secLayerMatrix,则两层matrix大小为:20*20*4byte+100*100*4byte即为0.04m。
所以16个线程下,总内存为:原地图阻挡信息0.5m、旋转地图阻挡信息0.5m、连通区信息2m、两层matrix0.04m*16,共3.64M,游戏中场景最多不到20个,所有场景JPS总内存为72.8M。
1.1.4.2内存池
在JPS搜索过程中,每次将一个跳点加入openset,都需要new出对应的节点对象,节点对象中存节点id、父节点、寻路消耗等共12个byte,为了减少内存碎片,以及频繁new的时间消耗,需要自行管理内存池,每次new节点对象时,均从内存池中申请,内存池详解请见下文服务器内存优化,为了防止内存池增长过大,需要限制搜索步数。
本文的内存池共有两个:
一,跳点的内存池,初始大小为800个跳点,当new的跳点数目超出800个,即停止寻路,因为服务器用JPS进行NPC的寻路,NPC不会进行长距离寻路,假设NPC寻路上限距离是20m,则寻路区域面积是40m*40m,格子数80*80即6400,经统计跳点数目占所有格子数目的比例不到1/10,即跳点数目少于640,因此800个跳点足够使用,800个跳点共占内存800byte*12,即为9.6k,忽略不计;
二,secLayerMatrix指向的100*100*4byte的内存池,因为每次寻路都需要至少一个secLayerMatrix,如果每次寻路都重新申请,寻路完后再释放,会造成开销,因此secLayerMatrix指向的100*100*4byte的空间也在内存池中,申请时,从内存池拿出,释放时,放回内存池即可,secLayerMatrix内存池占内存0.04m。
1.1.5路径优化
如图1.1.4.1所示,绿色格子为起点,红色格子为终点,灰色格子为跳点,蓝线为JPS搜出来的路径,灰色虚线为搜索过程。可以看出,从绿色格子到红色格子可以直线到达,而JPS搜索出来的路径却需要转折一次,在游戏表现上,会显得比较奇怪。因此在JPS搜索出来路径后,需要对路径进行后处理。
比如JPS搜出来的路径有A、B、C、D、E、F、G、H八个点,走到A时,需要采样检查A、C是否直线可达,如果A、C直线可达,再检查A、D是否直线可达,如果A、D直线可达,继续检查A、E,如果A、E直线不可达,则路径优化为A、D、E、F、G、H,走到D时,再检查D、F是否直线可达,如果D、F直线可达,继续检查D、G,如果D、G直线不可达,则路径优化为A、D、F、G、H。依此类推,直到走到H。因为采样检查的速度很快,大约占JPS寻路时间的1/5,而且只有当走到一个路点后,才采样检查该路点之后的路点是否可以合并,将采样的消耗平摊在行走的过程中,因此采样的消耗可以忽略。
图1.1.4.1
1.2视野管理算法的优化
1.2.1视野管理算法的背景
1.2.1.1九宫格
游戏中地图用来承载阻挡、静态建筑、NPC(非玩家控制角色:Non-Player-Controlled Character)、WRAP点等。玩家在地图上移动,其可见的其他玩家即发生变化,如果玩家的每次移动,都更新视野列表,时间成本太高,因此只有当玩家离开某个区域时,才更新视野列表,而在这个区域内的移动,并不更新视野列表。为了划分这个区域,引入九宫格概念,如图1所示,九个格子的总面积大于一个手机屏幕,小于两个手机屏幕。大于一个手机屏幕的原因是,可以预先计算当前屏幕外的一些玩家,但又没有必要预先计算太多的屏幕外玩家,因此小于两个手机屏幕,玩家可见的范围为以玩家为中心周围九个格子内的其他玩家。
如果玩家Me在格子5内移动,则不主动更新视野列表,玩家可见范围为红色和绿色格子内的玩家(如果玩家Me视野列表内的玩家He从一个格子移动到另一个格子,导致Me和He不可见,也会导致玩家Me的视野列表发生更新,称为被动更新),如果玩家Me从格子5移动到格子8则主动更新视野列表,玩家可见范围为紫色和绿色格子内的玩家。
图1.2.1.1.1玩家从九宫格的格子5移动到格子8
1.2.1.2视野管理的必要性
在大型多人在线游戏MMO(Massively Multiplayer Online)中,多个玩家在同一场景,此时玩家需要能看到其附近的玩家,同时不需要看到与其距离远的玩家。这就是视野管理需要做的事情:为每个玩家维护一个视野列表,管理每个玩家可见视野内的其他玩家。
MMO游戏中,视野对服务器造成的压力主要来源于两点:一,玩家频繁移动造成视野列表的频繁更新的压力;二,广播视野列表的带宽压力。因为视野列表中的玩家频繁变化,有的玩家离开当前玩家的视野,有的玩家新进入当前玩家的视野,因此当前玩家的视野列表需要进行频繁的增、删、查操作,因此增、删、查操作的时间复杂度要尽可能的低,从而缓解视野列表频繁更新的压力。
如果当前视野列表中有100个玩家,每个玩家都移动了一段距离,为了让其他玩家看到自己的移动,每个玩家都需要被通知其他99个玩家的移动,这就需要广播100*99个数据包,随着地图中玩家数目增加,造成广播量急剧增加,对带宽造成极大压力,因此玩家的视野列表需要有规模限制,从而缓解带宽压力。
本文提出一种利用全局内存池、双向链表、位标记进行视野管理的算法,可以将每次增、删、查视野列表的复杂度降为O(1)。
1.2.2全局内存池
全局内存池中存放的元素如图1.2.1.1所示。ViewLinkNodePair中有两个ViewLinkNode类型元素,ViewLinkNode定义如图1.2.1.2所示,记录ViewLinkNodePair指针类型的m_Parents,以及Obj_User指针类型的m_pUser,m_pUser即为指向玩家的指针。ViewLinkNodePair两个ViewLinkNode元素各自包含一个m_pUser指针,这两个m_pUser指针存放相互可见的两个玩家。采用内存池好处是避免内存碎片、以及频繁分配的消耗。
图1.2.1.1
图1.2.1.2
1.2.3双向链表
每个玩家的视野列表是一个双向链表,双向链表中每个元素包含ViewLinkNodePair中的两个ViewLinkNode之一,ViewLinkNode中记录ViewLinkNodePair和可见的玩家。当玩家A和B相互可见时,申请ViewLinkNodePair,A的ViewLinkNodeA记录ViewLinkNodePair和B,B的ViewLinkNodeB记录ViewLinkNodePair和A。当玩家A和B不相互可见时,在A的双向链表中找到记录B的ViewLinkNodeA,然后从A的双向链表中删除,并在记录B的ViewLinkNodeA中找到ViewLinkNodePair,在ViewLinkNodePair中找到记录A的ViewLinkNodeB,在B的双向链表中删除。
双向链表每个元素是CChainItem<ViewLinkNode>的指针,类模板CChainItem定义如图1.2.2.1所示,data存的是ViewLinkNode的指针。如图1.2.2.2所示,当两个玩家rObjA、rObjB相互可见时,首先从全局内存池g_ViewLinkPool新建一个对象,对象的指针为pPair,将pPair的m_LinkNodeA的m_pUser指向rObjB的地址,m_LinkNodeB的m_pUser指向rObjA的地址,m_Parents指向pPair。当两个玩家rObjA、rObjB相互不可见时,只需要在rObjA的双向链表中找到对应的CChainItem<ViewLinkNode>的指针,该指针的m_LinkNodeA中的m_pUser指向rObjB的地址,并将对应的双向链表的元素从rObjA的双向链表中删除,然后根据m_LinkNodeA的m_Parents找到对应的pPair,再从pPair中找到m_LinkNodeB,m_LinkNodeB的m_pUser指向rObjA的地址,将m_LinkNodeB从rObjB的双向链表中删除。
图1.2.2.1
图1.2.2.2
1.2.4位标记
游戏中需要频繁的判断两个玩家是否相互可见,然而采用全局内存池+双向链表的数据结构,最快只能采用遍历双向链表的方法,该时间复杂度为O(n),因此采用第三个数据结构:位标记辅助完成这项工作。每个场景中的Obj数量是有限的,我们游戏每个场景的Obj数目最大为2048,ObjID编号从0到2047,每个玩家是否可见用一个bit表示。所以每个玩家共需要2047个bit表示是否与其他2047个Obj可见,即0.25K,3000个玩家同时在线,位标记占0.75M。假设He的ObjID为10,判断Me是否可见He,只需要查看Me的第10个位标记是否为1即可。
1.2.5视野管理流程
如图1.2.1.1.1所示,玩家Me从格子5移动到格子8,老视野可见的玩家为红色和绿色格子内的玩家,新视野可见的玩家为紫色和绿色格子内的玩家。首先遍历Me的双向链表,对所有老视野列表的玩家打上标签1,然后遍历紫色和绿色格子内的玩家,如果玩家He已打标签1,则将玩家He打上标签2,说明玩家He在新视野和老视野都可见;如果玩家He没打标签1,则说明玩家He是新进视野的玩家,加入EnterList;重新遍历Me的双向链表,如果玩家He仍然是标签1,说明玩家He只在老视野,没在新视野中,加入LeaveList,同时记录玩家He在玩家Me视野数组中的索引。
例如Me在格子5时老视野列表里的玩家为:User1、User2、User3、User4、User5、User6;Me移动到格子8时,紫色和绿色格子内的玩家有User3、User4、User5、User6、User7、User8。首先对双向链表User1到User6六个玩家打标签1;然后对User3到User8打标签,因为User3到User6已打标签1,所以对这4个玩家打标签2,而User7、User8没打标签1,所以这两个玩家加入EnterList;再遍历双向链表User1、User2因为仍然是标签1,所以将这两个玩家加入LeaveList,同时记录这两个玩家的pPair。
对LeaveList的两个玩家User1、User2,因为已知pPair,所以已知Me和User1、User2三个玩家的双向链表中CChainItem<ViewLinkNode>的指针位置,删除即可。
对EnterList中的玩家,需要按照优先级高低放到不同的桶里,比如队友的优先级比其他玩家优先级高。然后按照优先级高低的顺序加入视野列表,如果视野列表已满,优先级高的玩家仍然没进入视野列表,需要从视野列表中删除优先级低的玩家,以便腾出空间将优先级高的玩家加入。对EnterList的两个玩家User7、User8,新建ViewLinkNodePair,并将ViewLinkNode插入对应的双向链表即可。
1.3玩家属性同步的优化
1.3.1背景介绍
本文适用于所有脏标记遍历功能,提升性能几十倍,本文以游戏中玩家的属性同步作为例子进行介绍。
MMORPG游戏中玩家有大量属性需要从服务器同步给客户端,例如名字、血量、战力、等级、速度等等。每当某个玩家的某个属性发生变化时,需要将玩家该属性的标志位置脏,在心跳或者其他需要发送的时机,调用同步属性函数,判断置脏的属性并同步给所有客户端。需要注意,不能每次在某个玩家的某个属性发生变化时,均同步给所有客户端,因为开销太大,一般在心跳里(固定时间间隔)同步。为了保证玩家属性在所有客户端及时更新,心跳间隔一般在500ms左右,如此频繁的调用以及同步属性函数内大量的脏标记判断导致同步属性函数成为性能瓶颈之一,大约占后台性能消耗的10%。
假设玩家有n个属性,k个属性置脏,最直观的做法是遍历所有n个属性,逐个判断是否置脏,置脏的属性同步给客户端,需要判断n次;本文作者之前提过一种优化算法,根据属性置脏的频率,优先判断置脏频率高的属性,当判断出的脏属性数目等于k,则停止,该优化效率显著优于遍历n个属性,但也不是最优的算法。
还有一种优化思路是用set记录置脏的属性,set插入时间复杂度为O(logn),置脏m个属性,set插入操作总时间复杂度为O(log(1*2*..*m)),再考虑某个属性频繁置脏的情况,比如第m个属性在同步之前置脏p次,则set操作时间复杂度为O(log(1*2..*m*p),虽然一般情况下m比较小,但不排除某些情况m很大,就会导致出现性能瓶颈,实测中发现采用set,o2编译,如图1.3.1.1所示插入50个脏属性耗时165639微秒,如图1.3.1.2所示置脏50个标记位耗时1522微秒,set效率低108倍,虽然同步的时间间隔内更新的属性数目很少,但某个属性更新的可能非常频繁,所以同步时间间隔内假设插入50个脏属性模拟很合理。
显然,如果算法无论属性更新是否频繁,无论属性数目是多是少,都能在k的时间判断出哪些属性置脏,则该算法为最优算法。因为置脏的属性非常稀疏,k往往是个位数,所以最优算法可以将效率提升几十倍。
图1.3.1.1
图1.3.1.2
1.3.2优化算法
为引出本文的优化算法,本文首先介绍一个问题:计算一个整数的二进制表示中有多少个1。基本做法如图1.3.2.1所示。假设该整数n为10001100,则需要右移7次。但计算机里的数字本来就是用二进制存的,所以计算过程也都是二进制计算。利用一些位运算的特性,可以很容易计算1的个数。该例子中n-1为10001011,n&(n-1)为10001000,可以看到低3位都变成了0。多验证几个例子,可以看出结论,要消除整数n最低位的1,可以使用n=n&(n-1)。从而计算n的二进制表示有多少个1的算法如图1.3.2.2所示。
图1.3.2.1
图1.3.2.2
本文介绍一个gcc的内置函数,__builtin_ffs(uint32 n),返回n最后一个为1的位是从后向前的第几位,例如若n为10001100,则__builtin_ffs(n)为3,该函数对应的x86汇编代码,O0编译结果如图1.3.2.3所示,仅有四条汇编指令。该内置函数64位的版本为__builtin_ffsll(uint64 n)。
图1.3.2.3
接下来正式介绍本文的优化算法,假设有64个属性,该64个属性用bit位表示是否置脏,共需64bit,将64bit转成uint64的n,每次用__builtin_ffsll找出最低位的1的位置,即可找出一个置脏的属性,然后用n&(n-1)消除最低位的1,当n为0时算法终止。假设64个属性第2个属性和第9个属性置脏,则该64bit编码为0...0100000010,首先用__builtin_ffsll找出低第2位的置脏属性,然后n=n&(n-1),即0...0100000000,再用__builtin_ffsll找出低第9位的置脏属性,然后n=n&(n-1)即为0,算法终止,可看出从64个属性里找出置脏的两个属性,只需要两次操作。
找出置脏属性后,使用switch语句而不是if语句处理需要同步的属性。因为随着if语句数目增多,效率会线性降低。而switch语句在case多的情况下(gcc在O0编译,case大于等于5个),翻译的汇编代码会使用查找表,在O(1)时间内找到对应的case,所以switch语句不会在case规模很大的情况下降低效率;在case很少的情况下(gcc在O0编译,case小于5个),仍然会逐个比较。需要注意,为尽可能提升性能,脏标记数目最好为64位整数倍,否则假如脏标记数目为120位,取出64位后,需要将剩下的63位拆分成32位、16位、8位,分三次取出,再计算脏标记位置,性能会降低。
1.3.3性能对比
num类型为uint64,记录所有脏标记,num低第2位、低第64位置脏,即num为100...010。图1.3.3.1所示为遍历所有属性,并逐个判断是否置脏,num&1不为0时,表示第j个属性被置脏,图1.3.3.2所示为采用本文的优化算法,index为最低位的脏标记的位置。实测中图1.3.3.1耗时2011微秒,图1.3.3.2耗时26微秒,性能提升77倍。本文的优化算法不仅适用于属性同步,所有脏标记相关的功能均可采用,例如数据的判断置脏并落地存储。
图1.3.3.1
图1.3.3.2
1.4跨服战团匹配算法的优化
游戏中存在跨服战等需求,将一些队伍组成固定规模战团,然后战团之间战斗,战团匹配过程应当尽量高效、快速,同时实现战力均衡。为了实现尽可能公平均衡的战团匹配,直观的做法当然是搜索所有队伍组成固定规模的战团,然而其时间复杂度为指数级,以极高的计算代价换取最优匹配显然是不现实的,因此,战团匹配问题也成为制约服务器性能瓶颈问题。
为此,本文利用压桶法实现了快速组成固定规模为K的战团,在尽量保证匹配战团的战力均衡前提下,将战团匹配的时间复杂度降为O(n)。具体上,当有玩家或队伍(实际中,队伍人数为1到5)申请组成战团时,将其加入队列尾部。然后在游戏的心跳中遍历队列,如果当前遍历的玩家或队伍的人数加上桶里的人数小于等于K,则将当前玩家或队伍加入桶,并从队列中删除;否则新建一个桶,将玩家或队伍加入新桶中。在战团匹配时,找出所有人数为K的桶,将桶里所有玩家的战力值的和设为对应桶的权重值,并以此对所有的满的桶进行排序,每次选择战力值最接近的两个战团进行战力均衡的调整,然后传送到战斗服务器进行战斗。
然而,由于压桶法是为了节省时间而选择的贪心算法,可能会遗漏能组成战团的玩家或队伍,因此在压桶法后,本文采用查表法对剩余的玩家和队伍再次尝试组成固定规模的战团。首先在服务器启动时做些预处理,群举所有能组成两个固定规模战团的组合(队伍人数为一的队伍数目,队伍人数为二的队伍数目,...,队伍人数为五的队伍数目),并存在set里,该步骤是全局唯一的,并且只需要做一次。然后统计剩下的玩家和队伍,计算人数为一、二、...、五的队伍数目。如果剩下的玩家或队伍队伍人数为一到五的队伍数目均大于set中某个元素,则set中该元素表示能组成两个固定规模战团的组合,并从剩下的玩家或队伍中删除。此步骤重复进行,直到剩下的玩家或队伍无法组成两个固定规模的战团。
通过上述方法,本文实现尽可能合理的战团组成,在此之后,为了尽可能实现两个战团战力均衡,本文进一步设计战团玩家调整方法。当两个固定规模的战团组成后,通过查询预先生成的表,调整两个战团里的玩家,使得两个战团的战力尽可能相等,增强战斗刺激性。具体上,首先群举所有的能组成两个固定规模战团的可能,并存在map里,map的key为字符串,key唯一标识战团的构成(队伍人数为一的队伍数目,队伍人数为二的队伍数目,...,队伍人数为五的队伍数目),map的value为一个vector容器,vector中存储当前key拆分成两个固定规模战团的所有可能。当调整两个战团的战力时,通过map查询当前两个战团能重组成的所有两个战团的可能,然后遍历所有的可能,找出两个战团战力最接近的组合。
1.5发包逻辑拆分
在服务器给客户端发包时,需要将数据包打包成流,在Encode操作中存在大量memcpy操作,而每个memcpy时间复杂度为O(n),因此打包过程也成为性能瓶颈之一。因此,本文认为有必要将数据包打包并发包的过程从游戏主线程中拆分,另开一个线程处理。在具体的多线程实现过程中,在主线程和发包线程之间需要有通信的数据结构,主线程负责将数据包写进该数据结构,发包线程负责将包从该数据结构中读取、打包、发送,合理的通信数据结构的使用将对多线程效率影响很大。
简单的实现可以采用c++的queue作为两个线程通信的数据结构,然而需要对queue加锁,才能保证两个线程读写安全,但锁的开销会降低性能。因此,本文采用基于字节流的无锁循环队列。因为每个数据包大小不一样,小的几个Byte,大的几百K,因此不能采用基于对象的无锁循环队列,否则几个Byte的数据包也会占据几百K的空间。
另外本文采用Tconnd作为网络通信组件,Tconnd发包需要携带TFRAMEHEAD,该结构体大小为12K,除了TFRAMEHEAD_CMD_START等管理包的该TFRAMEHEAD是从Tconnd接收然后再自己填充一些字段外,其他数据包的TFRAMEHEAD完全是自己拼的,因此知道需要填充哪些字段。所以除了TFRAMEHEAD_CMD_START等管理包的TFRAMEHEAD是在主线程收到并拼完,然后12K完整的写进无锁循环队列,其他的TFRAMEHEAD均是主线程将需要的参数写进无锁循环队列,发包线程再根据这些参数拼TFRAMEHEAD。这种优化可以大大降低无锁循环队列所占内存。
1.6玩家Cache
在当前多进程的服务器的架构下,查看玩家信息亟需优化。当一台服务器(GameServer1)的玩家要查看另一台服务器(GameServer2)的玩家信息时,需要经过多个服务器的多次查询中转。譬如,上述请求的流程可能为GameServer1->WorldServer->GameServer2->WorldServer->GameServer1,请求消息共需要转发四次。同时,查看离线玩家信息时,通常需要对数据库进行操作,这都导致查看玩家信息需要被优化。
为此,本文通过对玩家信息进行缓存(玩家cache)实现玩家信息查看优化。具体上,1)同一游戏服务器下的用户不需缓存,譬如,GameServer1玩家A查看GameServer1的玩家B不通过缓存就可以很容易地获取玩家B信息;2)不同游戏服务器下需进行玩家缓存,且缓存按需更新。譬如,GameServer1玩家A查看GameServer2的玩家C,在GameServer1的玩家cache中查看玩家C,如果玩家C进入缓存时间超过10秒,更新缓存中玩家C信息,如果玩家C不在缓存中,则从数据库加载;3)查看离线玩家同样利用玩家cache,每逢玩家离线,通知所有GameServer更新玩家cache中该玩家信息。
因为被查看的玩家往往都是等级、战力等特别高的玩家,这些玩家会被大量玩家查看,所以本文提出的玩家缓存机制往往命中率极高,实测中缓存命中率达到80%-90%左右。
二、服务器内存优化
2.1内存统计
在对内存优化之前,需要先确定程序每个模块的内存分配。程序的性能有perf、gprof等分析工具,但内存没有较好的分析工具,因此需要自行统计。在linux下/proc/self/statm有当前进程的内存占用情况,共有七项:指标vsize虚拟内存页数、resident物理内存页数、share共享内存页数、text代码段内存页数,lib引用库内存页数、data_stack数据/堆栈段内存页数、dt脏页数,七项指标的数字是内存的页数,因此需要乘以getpagesize()转换为byte。在每个模块结束后统计vsize的增加,即可知该模块占用的内存大小。
在面向对象开发中,内存的消耗由对象的消耗组成,因此需要统计每个类的成员变量的占用内存大小。使用CLion或者visual studio都可以导出类中定义的所有成员变量,然后在gdb使用命令:
p((unsigned long)(&((ClassName*)0)->MemberName)),即可打印出类ClassName的成员变量MemberName相对类基地址的偏移,根据偏移从小到大排序后,变量的顺序即为定义的顺序,根据偏移相减即可得出每个成员变量大小,然后优化占用内存大的成员变量。
2.2内存泄露
内存泄露是指程序中已动态分配的堆内存由于某种原因程序未释放或无法释放,导致内存一直增长。虽然有valgrind等工具可以检查内存泄露,但valgrind虚拟出一个CPU环境,在该环境上运行,会导致内存增大、效率降低,对于大规模程序,基本无法在valgrind上运行。因此需要自行检查内存泄露,glibc提供的内存管理器的钩子函数可以监控内存的分配、释放。如图2.2.2、2.2.3所示,分别为钩子函数的分配内存和释放内存。因为服务器启动时需要预先分配很多内存,比如内存池,这些内存是在服务器停止时才释放,因此为了避免这些内存的干扰,在服务器启动之后才能开始内存泄露的统计。
首先申请固定大小的vec_stack,记录所有分配的内存,如果有释放,则从vec_stack中删除,最后vec_stack中的元素即为泄露的内存,vec_stack必须为固定大小,否则vector扩容中会有内存分配,也不可以用map,map的红黑树旋转也会有内存分配,会造成干扰;然后通过图2.2.1所示的my_back_hook记录原有的malloc、free;并通过图2.2.2所示的my_init_hook将malloc、free换成自定义的钩子函数。
每次分配内存时,都会进入自定义钩子函数my_malloc_hook中,如图2.2.2所示。在my_malloc_hook中首先通过my_recover_hook将malloc恢复成默认的,否则会造成死递归,然后通过默认的malloc分配大小为size的空间,为了分线程统计内存泄露,还需要对线程号做判断,在stTrace.m_pAttr记录内存分配的地址,m_nSize记录大小,m_szCallTrace记录调用栈,如果vec_stack已满,需要根据m_nSize从大到小排序,如果当前分配内存大于vec_stack记录的最小的分配内存,则替换;如果未满,则直接加入vec_stack,在my_malloc_hook结束时,将malloc替换成自定义的malloc。
每次释放内存时,都会进入自定义钩子函数my_malloc_free中,如图2.2.3所示。在my_malloc_free中首先通过my_recover_hook将free恢复成默认的,否则会造成死递归,对线程号判断,然后在vec_stack中删除对应的分配,并将free替换成自定义free。
图2.2.1
图2.2.2
图2.2.3
2.3内存池
在游戏服务器内存分配过程中,glibc中的malloc采用的是ptmalloc,ptmalloc在对小对象进行分配时会产生大量内部碎片,同时也会有外部碎片的产生。因此往往需要自行设计并实现模板化的内存池,采用内存池的好处是,避免内部、外部碎片,对象New/Delete均为O(1)复杂度,同时有利于监控。例如当模板参数为宠物时,首先new出60个宠物的空间,对这60个宠物空间,当60个空间被全部使用时,再分配60个空间。本文在内存池设计中实现两个数据管理器,分别是空闲数据管理器freeList和使用空间管理器usedList,freeList采用queue实现即可,usedList采用vector。
由于这部分较复杂,因此用代码辅以说明。如图2.3.1,在Init函数中传入要创建的对象数目capacity,pointer根据capacity预先分配空间,用于建立所有对象索引,pointer主要用来校验。本文按块Chunk创建对象,每块Chunk有objectperchunk个T类型对象。chunksize记录当前总共创建了多少对象。虽然Init函数设定了capacity,但是初始并没有创建capacity个T对象,而是先创建objectperchunk个T对象供使用,并记录到freelist中。
如图2.3.2所示,每次新创建对象时调用NewObj函数,如果freelist为空,说明所有已创建的对象均被使用,则再调用NewChunk创建objectperchunk个T对象;如果不为空,直接返回freeList头部的指针。
如图2.3.3所示,每次删除对象时调用DeleteObj函数,参数为待删除对象指针,除了必要的校验以外,将对象指针从usedList删除,并将usedList最后一个对象指针移动到删除位置,记录删除位置deleteusedlistindex。同时将对象指针所指的对象清空加入freeList,以便再次使用,好处时内存不回收可以重复使用。
如图2.3.4所示,对象的遍历在usedList上进行,但在遍历中可能会删除对象,此时deleteusedlistindex==iterateindex,因为删除对象后,会将usedList最后一个对象指针移动到deleteusedlistindex位置,因此iterateindex不能增加。
图2.3.1
图2.3.2
图2.3.3
图2.3.4
2.4内存分配(ptmalloc vs tcmalloc)
即使使用内存池,程序中仍然需要大量使用malloc分配空间。但主流使用的ptmalloc存在如下缺点:一,ptmalloc采用多个线程轮询加锁主分配区和非主分配的方式,造成锁的开销;二,多线程间的空闲内存无法复用,利用线程A释放一块内存,由于并不一定会释放给操作系统,线程B申请同样大小的内存时,不能复用A释放的内存,导致使用内存增加;三,ptmalloc分配的每块chunk需要8个字节记录前一个空闲块大小和当前块大小以及一些标记位。
为此,本文提倡使用tcmalloc进行内存分配。tcmalloc对每个线程单独维护ThreadCache分配小内存;针对ptmalloc多线程内存无法复用的问题,tcmalloc为进程内的所有线程维护公共的CentralCache,ThreadCache会阶段性的回收内存到CentralCache;针对ptmalloc每块chunk使用8个字节表示其他信息,tcmalloc对每块chunk使用大概百分之一的空间表示其他信息,对小对象分配,空间利用率远高于ptmalloc。
三、服务器启动时间优化
3.1读取阻挡文件优化
服务器启动时,需要读大量文件,其中最大的文件就是阻挡文件,每个阻挡文件大约有几M,采用c++的ifstream可以一次读取一个字节,也可以一次读取整个文件,后者的速度比前者快几十倍以上。如图3.1.1所示,MATRIX_LEN为4096,阻挡文件为4096*4096byte,共16M,图3.1.1按byte读取阻挡文件需要2564ms,图3.1.2一次性读取阻挡文件需要50ms。
本文节选自《2018腾讯移动游戏技术评审标准与实践案例》 点击下载》》》https://tig.qpic.cn/doc/2018腾讯移动游戏技术评审标准与实践案例.pdf
|