|
|
template <class T, class FAdd, class FElem> T For(int from, int to, FAdd fAdd, FElem fElem)
{
assert(to >= from);
T sum = fElem(from);
for (int i = from + 1; i <= to; i++)
sum = fAdd(sum, fElem(i));
return sum;
}
数学上面我们常看到这样的符号,比如:
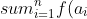\\&space;\\&space;\\&space;\\&space;\\bigcap_{k=0}^{m}X_{k})
这两个分别是求一串式子的和,和一串的集合的并。
类似地,我们可以从求和、求并,推广到任意的二参数运算(或二参数函数)
比如推广到字符串加
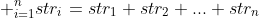
再比如更复杂的,字符串之间以 "," 相连,例如我们要生成一个表示一个数组的字符串,
例如 to_str(x[0]) + "," + to_str(x[1]) + "," + ... + "," + to_str(x[n-1])
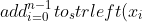\\&space;where\\&space;add\\left&space;(&space;a,b&space;\\right&space;)\\&space;=\\&space;a&plus;","&plus;b)
这个计算,用我们在本文开头定义的 For 函数可以写成:
str add(str a, str b) { return a + "," + b; }
For(0, n-1, add, [](int i){ return to_str(x); })
// 或者:
For(0, n-1, [](str a, str b) { return a + "," + b; }, [](int i) { return to_str(x); })
PS. 有时候考虑到性能,我们还可以有一种变种版本:
template <class T, class F> T For(int from, int to, T sum0, F f)
{
if (to < from)
return sum0;
T sum = sum0;
for (int i = from; i <= to; i++)
sum = f(sum, i);
return sum;
}
这里的 f 就是上面的 fAdd(求和) 和 fElem(求第i个元素) 的复合函数,
比如上面的那个计算可以改写成:
For(0, n-1, "", [](ptr<str> pSum, int i) { *pSum += to_str(x); return pSum; })
不过必须注意,这种情况下,参数 sum0 必须为你那个(T上的)"加法"运算的"单位元",或者是被"加"的第一个元素。
举个典型的例子,计算 a[0] * a[1] * ... * a[n-1]
如果写成 For(0, n-1, 0, [](float product, int i) { return product * a; })
这样就错了!
应当写成 For(0, n-1, 1, [](float product, int i) { return product * a; }),
或者 For(1, n-1, a[0], [](float product, int i) { return product * a; }). |
|